Optimizing under Uncertainty: the Price of Robustness in Planning and Beyond

To plan a large-scale project, design a supply chain, manage an investment portfolio, or even configure airspace sectors for air traffic control. You likely rely on mathematical models – optimization tools – to find the best possible plan. Standard optimization often assumes we know all the input data precisely. For instance, a basic linear optimization problem seeks to maximize an objective $c'x$ subject to constraints $Ax \le b$. But what happens when the values in $A$, $b$, or $c$ aren't perfectly known?

In the real world, data is rarely exact. Costs fluctuate, demands vary, market returns are volatile, and air traffic deviates from forecasts. A plan deemed "optimal" on paper might become infeasible or perform poorly when faced with real-world uncertainties. This raises a critical question: How can we create plans that are robust to unexpected changes, without being overly cautious and sacrificing too much efficiency?

Groundbreaking work by Dimitris Bertsimas and Melvyn Sim (2004) tackled this challenge head-on. Their classic paper explores how to measure and adjust the "price" we pay in nominal performance for the benefit of robustness, proposing an fundamental approach that allows planners to flexibly control the level of protection against uncertainty while keeping the problem computationally manageable.

Background: The Challenge of Uncertainty in Optimization

Mathematical optimization, particularly linear programming (LP) and mixed-integer programming (MIP), are powerful tools. However, the assumption of precise data is a significant limitation. Acknowledging this, researchers developed "robust optimization."

Early methods, like Soyster's (1973), aimed for solutions feasible for all possible data variations within a defined set (e.g., each coefficient $\tilde{a}_{ij}$ can be anywhere in $[a_{ij} - \hat{a}_{ij}, a_{ij} + \hat{a}_{ij}]$). This often meant replacing $a_{ij}$ with its worst-case value, leading to guaranteed robustness but overly conservative solutions – sacrificing too much potential performance just to be safe under the absolute worst-case scenario.

Later methods (e.g., Ben-Tal & Nemirovski, 1998; El-Ghaoui et al., 1998) offered less conservative approaches, often using ellipsoidal uncertainty sets. These transformed linear problems into nonlinear ones like second-order cone programs (SOCP). While powerful, the increased computational difficulty limited their use, especially for large-scale problems or those involving discrete decisions (MIPs), which are common in areas like scheduling and resource allocation.

The Need for a Flexible, Tractable Bridge

There was a clear need for a method offering more flexibility than the ultra-conservative approaches but retaining the computational tractability of linear optimization, making it suitable for a wider range of real-world problems, including MIPs.

Methodology: Introducing Controlled Conservatism ($\Gamma$-Robustness)

Bertsimas and Sim introduced a novel concept: $\Gamma$-Robustness. Instead of guarding against all uncertain parameters $\tilde{a}_{ij}$ in a constraint $i$ (say, $\sum_j \tilde{a}_{ij} x_j \le b_i$) taking their worst-case values simultaneously, their method protects against a chosen number, $\Gamma_i$ (Gamma), of these parameters deviating adversely. $\Gamma_i$ acts as a "robustness budget" for constraint $i$.

Consider a constraint $i$ where coefficients $a_{ij}$ for $j$ in an index set $J_i$ are uncertain, varying within $[a_{ij} - \hat{a}_{ij}, a_{ij} + \hat{a}_{ij}]$. The core idea is to ensure the constraint holds even if nature chooses up to $\lfloor\Gamma_i\rfloor$ coefficients to change to their worst value ($a_{ij} + \hat{a}_{ij}$ if $x_j > 0$, or $a_{ij} - \hat{a}_{ij}$ if $x_j < 0$), and one additional coefficient $a_{it}$ changes partially by $(\Gamma_i - \lfloor\Gamma_i\rfloor)\hat{a}_{it}$.

Conceptually, the robust constraint becomes: $\sum_j a_{ij} x_j + \beta_i(x, \Gamma_i) \le b_i$

Here, $\beta_i(x, \Gamma_i)$ is the "protection function," representing the additional buffer needed. It's defined as the maximum possible impact of the allowed $\Gamma_i$ worst-case deviations.

Furthermore, the approach provides a probabilistic guarantee. If the uncertain parameters $\tilde{a}_{ij}$ are independent and symmetrically distributed around $a_{ij}$, the probability that the robust constraint $i$ is violated is bounded above by $B(n, \Gamma_i)$, where $n = |J_i|$. This bound, derived in the paper, is often very small even for moderate $\Gamma_i$.

Key Findings of Bertsimas & Sim (2004)

The original paper demonstrated several key advantages:

1. Tractable Robustness: The method produced robust solutions for both LPs and MIPs (like the knapsack problem) without requiring specialized nonlinear solvers.
2. Tunable Conservatism: The $\Gamma$ parameter effectively controlled the trade-off between robustness and nominal performance. Decision-makers could see the "price of robustness" – how much optimal value was sacrificed for a given level of protection $\Gamma$.
3. Practical Insights: The portfolio example showed how optimal strategies could shift (e.g., from high-return focus to diversification) as $\Gamma$ increased.

Application in Air Traffic Management

In my own research on Dynamic Airspace Configuration (DAC) (Lui et al., 2025), we faced the challenge of uncertain air traffic demand. The goal was to find a sequence of airspace configurations (sets of active sectors) over time to minimize total traffic excess (demand exceeding capacity), which acts as a proxy for delays. The objective function involved minimizing $\sum_{t,c} e_c(t) x_c^t$, where $x_c^t$ is a binary variable (1 if configuration $c$ is active at time $t$, 0 otherwise) and $e_c(t)$ is the nominal traffic excess for configuration $c$ at time $t$.

Since future traffic demand is inherently uncertain, $e_c(t)$ can deviate from its nominal value. We applied the Bertsimas-Sim framework by treating these $e_c(t)$ coefficients as uncertain within a range $[e_c(t), \bar{e}_c(t)]$. We introduced a single budget $\Gamma$ for the entire planning horizon. The $\Gamma$ parameter allowed us to control the level of conservatism in the configuration plan, protecting against up to $\Gamma$ configuration-time instances having higher-than-nominal traffic excess. The linear nature of the Bertsimas-Sim robust counterpart was essential for solving this large-scale scheduling problem efficiently, especially when integrated into a faster graph-based solution method we developed.

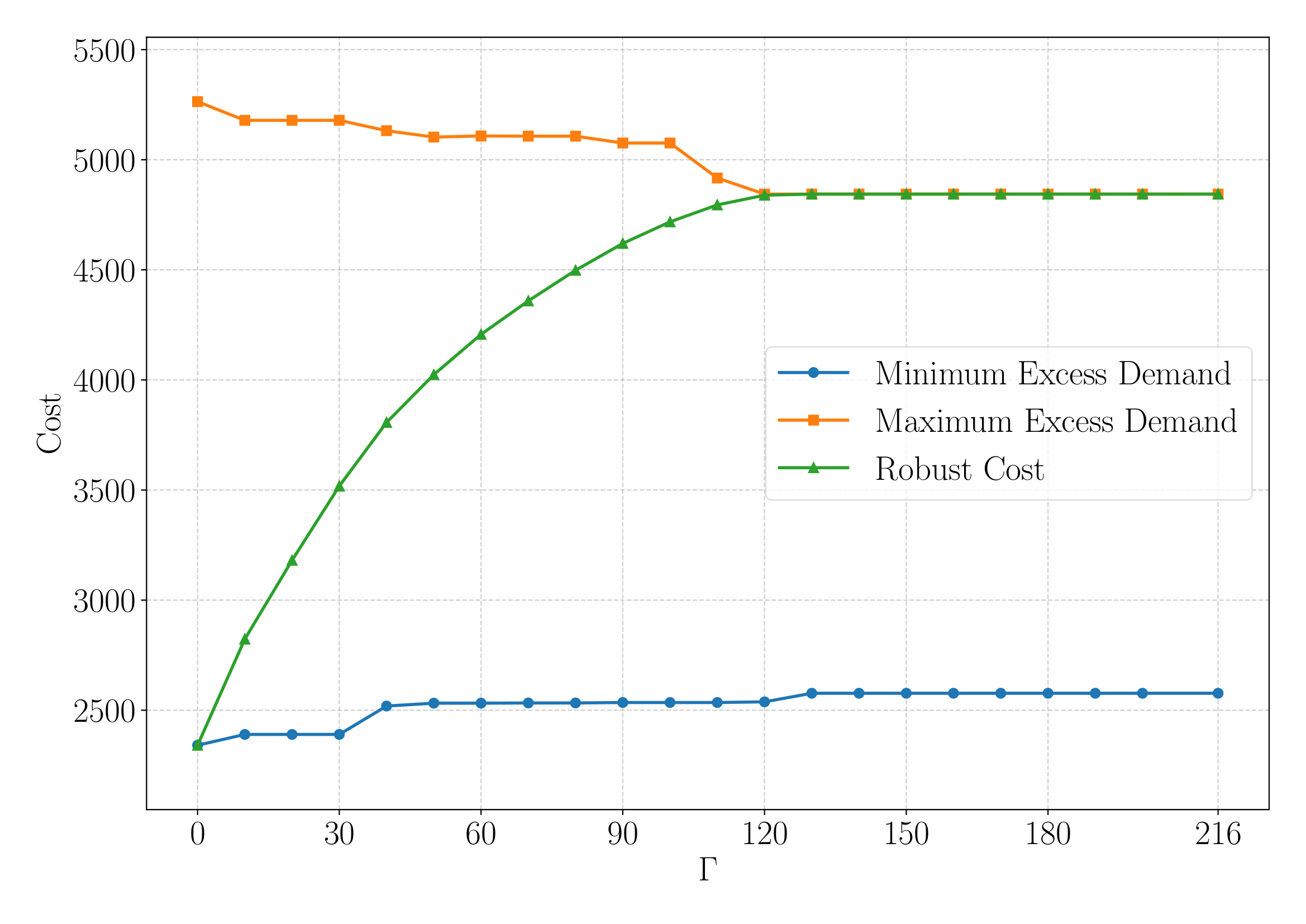
The figure above from our work in ATM (Lui et al., 2025) provides an illustration of robust optimization principle. The chart plots the total excess traffic demand realized under three different uncertainty scenarios: (i) the nominal scenario where all excess costs take minimum values, (ii) a more pessimistic scenario with maximum excess considered, and (iii) the worst-case scenario associated with each specific $\Gamma$ value (represented as the robust cost). As shown in the figure, the excess in the nominal scenario increases with $\Gamma$, while the excess in the more pessimistic scenario decreases with $\Gamma$. The robust cost follows a trajectory from the nominal minimum excess (at $\Gamma=0$) to the fully robust cost. This study confirmed the practical value of the Bertsimas-Sim approach: using $\Gamma$-robustness allowed us to create airspace configuration plans that demonstrably absorbed unexpected traffic better. The linearity also enabled us to use faster graph-based algorithms for the DAC problem, crucial for tactical deployment.

Implications

The Bertsimas-Sim approach offers significant practical value:

• Accessible Robustness: It provides a powerful yet computationally feasible framework for many LP/MIP problems under uncertainty.
• Informed Risk Management: The $\Gamma$ parameter gives managers a concrete lever to balance performance and risk, backed by clear deterministic and probabilistic guarantees.
• Enabling Robust Discrete Optimization: By preserving linearity, it greatly expands the applicability of robust optimization to scheduling, assignment, and facility location problems common in operations research.

From my perspective as an ATM researcher, the Bertsimas-Sim approach is particularly impactful. Air traffic operations require decisions made under significant uncertainty (weather, demand fluctuations).

Conclusion

Planning in the face of uncertainty is unavoidable. Relying on models that assume perfect data often leads to fragile solutions. The $\Gamma$-Robustness framework by Bertsimas and Sim provides an elegant, practical, and theoretically sound methodology to overcome this. By allowing tunable protection against uncertainty while crucially maintaining the computational advantages of linear optimization, it empowers decision-makers across various fields – from finance to logistics to air traffic management – to build plans that are not just efficient on paper, but resilient in the real world. It offers a way to intelligently manage the "price of robustness," ensuring our plans are better prepared for the future.

References

• Bertsimas, D., & Sim, M. (2004). The Price of Robustness. Operations Research, 52(1), 35–53. DOI: 10.1287/opre.1030.0065
• Lui, G. N., Lulli, G., De Giovanni, L., Galeazzo, M., Garcia-Ovies Carro, I., & Llorente Martinez, R. (2025). A robust optimization approach for dynamic airspace configuration. Accepted at ATM Seminar 2025, the first US-Europe Air Transportation Research & Development Symposium.